What is Voltage Law?
May 19, 2023This blog covers:
History and Definition
Kirchhoff's Voltage Law (KVL), also referred to as voltage law, is a fundamental principle in electrical circuit analysis. KVL was discovered by Gustav Kirchhoff, a German physicist, and he introduced it in 1845 as a fundamental principle in the analysis of electrical circuits. It is a mathematical expression that describes the behavior of electric circuits by stating that the sum of the voltage drops around a closed loop of a circuit must be equal to the sum of the voltage sources in the same loop (Nilsson & Riedel, 2015, 38). Another way to view this law is to relate it to the law of conservation of mass and energy: total voltage supplied to a circuit is equal to the total voltage used in the circuit.
Electrical circuit analysis is a fundamental aspect of electrical engineering that involves an analytical approach to understanding and evaluating the behavior inside of an electrical circuit. Analyzing electrical circuits involves examining the behavior of electrical signals as they travel through various circuit components: resistors, capacitors, inductors, and transformers. This analysis will include identifying the voltage and current characteristics, as well as power dissipation and energy transfer within the circuit.
Voltage law is essential to understand the behavior of electrical circuits-this is because it allows us to calculate the voltage at any point in a closed-loop circuit. Suppose we have a simple circuit with a battery, a resistor, and a switch. When the switch is closed, current flows through the resistor and a voltage drop will occur across the now activated resistor. KVL states that the sum of the voltage drop across the resistor and the voltage of the battery must be equal to zero.
Another way to understand KVL is by using the concept of potential difference. Voltage, also known as potential difference, is the difference in electric potential between two points in a circuit. In a closed loop, the potential difference between the starting and ending points must be zero since the voltage at the starting point is equal to the voltage at the ending point. Therefore, the sum of the voltage drops in a closed loop must be equal to the sum of the voltage sources in the same loop.
Kirchhoff's Voltage Law in a Series Circuit
To apply KVL in a series circuit, we can follow these steps:
1. Identify the closed loop(s) in the circuit.
2. Establish a direction to the current flowing in the loop.
3. Indicate the voltage drops across each component in the loop based on the current's direction. When the current flows from a positive terminal to a negative terminal, the voltage drop will be positive, but, if it flows from a negative terminal to a positive terminal, the resulting voltage drop will be negative.
4. Calculate the sum of the voltage drops around the loop and equate it to the sum of the voltage sources in the same loop.
Let's take a look at the example series circuit:
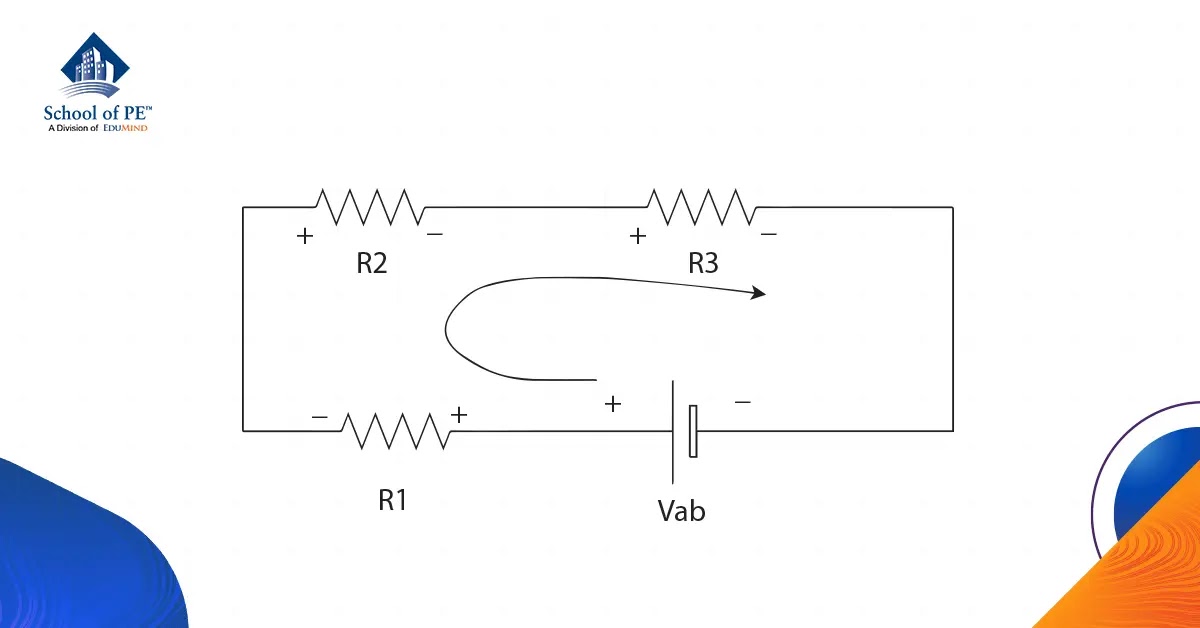
We use the steps above to analyze the provided diagram. The circuit shown is a closed loop series circuit, due to it forming a complete, unbroken path for the current to flow. We assign the direction to be clockwise, following the current path of the voltage source. Now based on step 3, we label the voltage drop across each component.
| Source | Voltage drop |
| Power source Vab | -Vab |
|
Resistor R1 |
+VR1 |
| Resistor R2 | +VR2 |
| Resistor R3 | +VR3 |
We can represent the KVL equations of the closed loop circuit as below:
-Vab + VR1+ VR2 + VR3 = 0
VR1 + VR2 + VR3 = Vab
To begin with, it is important to grasp the primary concept of parallel circuits, a parallel circuit is identified when the voltage is constant across all the elements present in the circuit. This is because in a parallel circuit, there are solely two groups of electrically connected points, and the voltage difference measured between these sets of points always remains identical at any particular moment.
Vab = VR1 = VR2 = VR3
From the above circuit, there are two connected points (across R1 and R2 ) being connected with the voltage source Vab . So, the voltage across R1 is equal to the voltage across R2 and R3 , hence equals to the voltage source Vab .
It is important to note that KVL only applies to closed loops, meaning that there must be a path for the current to flow back to its starting point (Nilsson & Riedel, 2015, 38). If there is an open loop, voltage law cannot be applied. KVL is an essential tool in electrical circuit analysis, as it allows us to calculate the voltage drop across any component in a circuit. KVL has many real-world applications, such as designing and analyzing circuits for electronic devices, power systems, and communication systems. Moreover, it is a crucial concept that everyone who is either working or pursuing a degree in the field of electrical engineering should be familiar with.
Other Applications
Applying KVL in an electrical power system, power engineers are able to maintain a balance between the energy supplied and the energy consumed. If the energy consumed is greater than the energy supplied, there is a significant voltage drop in the system, and this may lead to a system failure. To mitigate a potential system failure, power engineers use KVL to analyze the voltage drops across the apparatus power equipment and ensure that the power system is functioning correctly.
KVL is also applied within electronic device design, including, but not limited to, smartphones, computers, and appliances consisting of numerous circuits that are designed to perform specific functions. Engineers in this field will need to utilize KVL to ensure appropriate power is delivered to all the crucial components in a device; for a smartphone, that could be the screen, the speakers, GPS, communications, etc.
Conclusion
To summarize, Kirchhoff's Voltage Law is a fundamental principle in electrical circuit analysis that states that the sum of the voltage drops around a closed loop circuit must be equal to the sum of the voltage sources supplied in the same loop. By using this law, we can calculate the voltage(s) at any point in a circuit and analyze its behavior. KVL is a crucial concept for anyone working in the field of electrical engineering or pursuing a degree in this field.
References
Nilsson, J. W., & Riedel, S. A. (2015). Electric Circuits. Pearson.
Interested in pursuing a career as an electrical engineer? Sign up for an FE Electrical or PE Electrical exam review course with School of PE today and join our tens of thousands of students who have passed their engineering exams!
Latest Blogs
Blogs by Year/ Month
Copied to clipboard