What is Ohm's Law?
One of the most fundamental principles in electrical engineering is Ohm's law. Ohm's law plays a critical role in understanding the relationship between resistance, voltage, and current in electrical circuits. This fundamental law is a mathematical formula that calculates the behavior between these elements in a circuit (Nilsson & Riedel, 2015, 30). In this blog, we will explore Ohm's law in detail, including its history, definition, applications, and limitations.
This blog covers,
• History
• Electrical Resistance (Ohm's Law)
• Resistance in Series
• Resistance in Parallel
• Power
• Application
• Limitation
• Electrical Resistance (Ohm's Law)
• Resistance in Series
• Resistance in Parallel
• Power
• Application
• Limitation
History
Ohm's law was first discovered by German physicist Georg Simon Ohm in 1827 while investigating the behavior of electric currents through various materials. Ohm observed that the amount of electric current flowing through a conductor is proportional to the voltage applied across it, and inversely proportional to the resistance of the conductor (Nilsson & Riedel, 2015, 48). He characterized this relationship into a mathematical equation, which we now know as Ohm's law.
Electrical Resistance (Ohm's Law)
Resistance is a critical concept in electrical engineering that describes the ability of materials to impede the flow of electric charge. This behavior is modeled using a component called a resistor, which plays a crucial role in designing and analyzing electrical circuits. Understanding resistance involves visualizing the interaction between electrons that make up an electrical current and the atomic structure of the material they are moving through. While almost all materials exhibit some degree of resistance, the degree of resistance varies depending on the material. Materials with low resistance, like copper and aluminum, are commonly referred to as conductors and are ideal for conducting electricity through wiring due to their conductive properties.
To effectively analyze circuits, it is crucial to establish a reference point for the current in the resistor relative to the terminal voltage. There are two ways to accomplish this: by referencing the direction of the voltage drop across the resistor (right image) or by referencing the direction of the voltage rise across the resistor (left image). This is demonstrated in Figure 1 below.
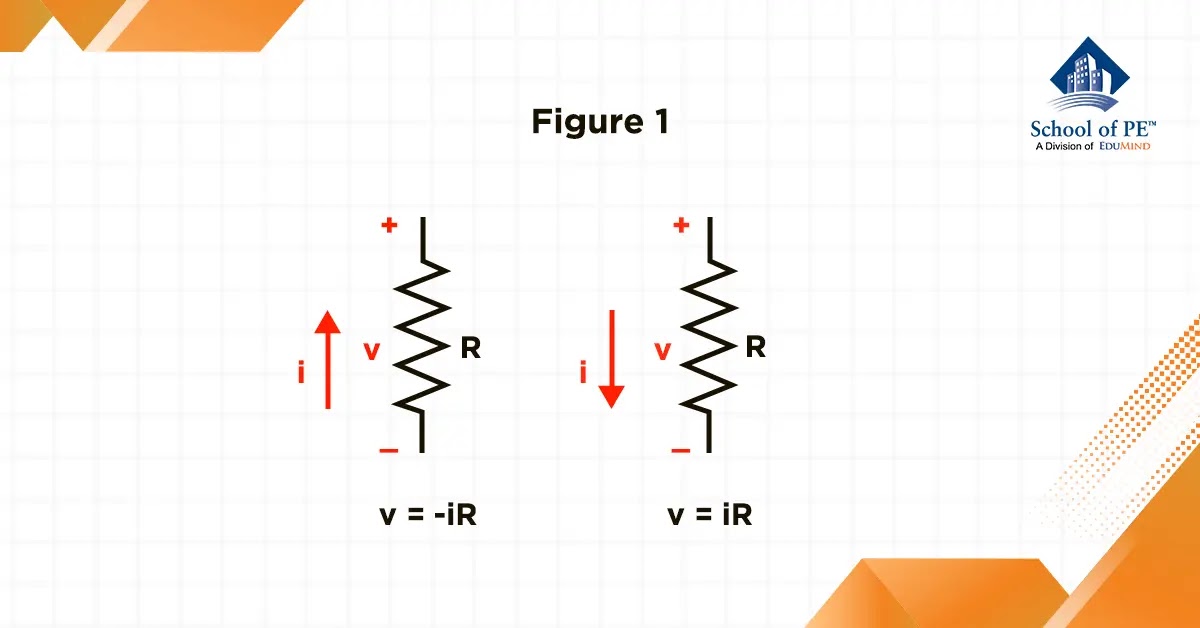

The equation for Ohm's law is:
V = iR (1)
where V is the voltage across the conductor, i is the current passing through it, and R is the resistance of the conductor. They are measured in volts, amperes, and Ohms, respectively. This equation shows that if the voltage across a conductor is increased, the current passing through it will also increase, as long as the resistance remains constant (Nilsson & Riedel, 2015, 48). Similarly, if the resistance is increased, the current passing through the conductor will decrease, as long as the voltage remains constant.
The inverse of resistance is conductance. It is denoted by the letter G, and is measured in siemens (S).
G = 1⁄R (S) (2)
Resistance in Series
The second principle of series circuits is that the overall resistance of a series circuit is equal to the summation of the individual resistances. This concept is relatively straightforward, as it follows that when the number of resistors in series increases, the flow of current becomes more challenging due to the greater resistance. Therefore, it intuitively makes sense that the total resistance in a series circuit will be equal to the sum of the individual resistances.

From Figure 2, the total resistance is:
R total = R1 + R2 + R3 (3)
Resistance in Parallel
As previously demonstrated with series resistor networks, the total resistance, Rtotal, of the circuit is equivalent to the summation of all individual resistors added together. However, with resistors in parallel, the equivalent circuit resistance, Rtotal, is calculated differently. Instead of summing the resistances themselves, we sum the reciprocal value 1⁄Rtotal of the individual resistances. The inverse of the algebraic sum then yields the equivalent resistance, as illustrated in the provided example. By utilizing this method, we can determine the total resistance of a parallel resistor network and better understand its behavior in electrical circuits.

From Figure 3, the total resistance is:
1⁄Rtotal = 1⁄R1 + 1⁄R2 + 1⁄R3
Power
Given the values of voltage, current, and resistance, it is possible to calculate the power at the terminals of a resistor using various methods. The fundamental equation for calculating power involves multiplying the terminal voltage and current. This value is expressed in units of Watts (W), a standard unit for measuring power.
p = vi (4)
By substituting Equation 1 into Equation 4, we can express the power of a resistor in terms of the current and resistance, providing a more concise and simplified means of calculating power in circuits.
p = vi = (iR)i = i2R (5)
Additionally, the power at the terminals of a resistor can be expressed in terms of voltage and resistance.
p = v(v⁄R) = v2⁄R (6)
Application
Ohm's law is a critical component in both electrical engineering and physics. For example, it can be used to design and analyze electrical circuits, determine the appropriate size and rating of electrical components, and troubleshoot and diagnose problems in electrical systems. It is also used in the development of electronic devices, such as transistors, diodes, and integrated circuits.
One of the most significant applications of Ohm's law is in the design and analysis of power distribution systems. Power transmission lines, transformers, and other components of electrical power systems must be designed to handle the amount of current that will flow through them under normal operating conditions. By using Ohm's law, engineers are able to calculate the expected current flow and voltage drop in a given component and choose the appropriate size and rating to ensure that it can handle the load of the system.
In addition, Ohm's law has many important implications for the safety of electrical systems. If the voltage applied to a circuit is too high, it can cause the current to increase beyond the capacity of the conductors and components, leading to overheating, damage, and even fires. By using Ohm's law to calculate the expected current flow and voltage drop in a circuit, engineers can design systems that are safe and reliable.
Limitation
However, Ohm's law has some limitations and assumptions that must be considered when using it to analyze and design electrical circuits. One of the main assumptions is that the conductor has a linear resistance, meaning that the resistance remains constant regardless of the current flowing through it. In reality, many conductors have nonlinear resistance characteristics, which can cause the current and voltage to behave in unexpected ways.
Another limitation of Ohm's law is that it only applies to DC circuits or circuits where the voltage and current are constant over time. In AC circuits, the voltage and current are constantly changing in magnitude and direction, which can cause the behavior of the circuit to be more complex and difficult to predict. However, Ohm's law can still be useful in analyzing AC circuits, as long as the behavior of the circuit can be simplified and modeled using equivalent circuits.
Conclusion
Ohm's law is a fundamental principle in electrical engineering and physics that describes the relationship between current, voltage, and resistance in a system. It provides a powerful tool for designing and analyzing electrical systems and has many important applications in power systems, electronics, and other fields. However, it also has some limitations and assumptions that must be considered when using it to analyze and design circuits. Despite these limitations, Ohm's law remains a cornerstone of electrical engineering and continues to be studied and applied by researchers and engineers around the world.
Do you want to become an electrical engineer? Sign up for an FE Electrical or PE Electrical exam review course with School of PE today!
References
Nilsson, J. W., & Riedel, S. A. (2015). Electric Circuits. Pearson.
